计算机图形学基础(1)——线性代数
最近对计算机图形学比较感兴趣,刷了一遍《计算机图形学入门:3D渲染指南》,看了一遍《GAMES 101》。本文对计算机图形学的线性代数相关基础进行了梳理和总结,以便后续进行复习和回顾。
点
点(Point)表示坐标系中的一个特定位置,其具体表示和抽象表示分别如下。
- 使用 大写字母 的方式来抽象表示一个点,如:\(P\)。
- 使用 圆括号 + 数字序列 的方式来具体表示一个点,如:\((4, 3)\)。
在具体表示中,数字序列的顺序很重要。按照惯例,在 2D 平面中依次表示 \(x\)、\(y\) 轴的值;在 3D 空间中依次表示 \(x\)、\(y\)、\(z\) 轴的值。对此,我们也可以结合两种方式来表示一个抽象的点,比如:\((P_x, P_y)\)。
向量
向量(Vector)表示两个点所构成线段的长度和方向,其具体表示和抽象表示分别如下。
- 向量的抽象表示一般有三种,分别是:
- 使用 小写字母 + 箭头上标 的方式,如:\(\vec{a}\)。
- 使用 加粗小写字母 的方式,如:\(\textbf{a}\)。
- 使用 两个点 + 箭头上标 的方式,如:\(\overrightarrow{AB} = B - A\)。注:大写字母表示点。
- 向量的具体表示中,默认以坐标原点作为起点,因此只需要描述终点即可。向量一般使用矩阵来表示,包含两种方式,分别是:
在定义中我们提到向量包含了两个点之间的长度和方向两种信息。对此,我们可以各自使用一种方式来表示这两种信息。
- 使用 小写字母 +
^上标 的方式表示 单位向量(Unit Vector),即长度等于 1 的向量,如:\(\widehat{a}\)。一般用来表示方向。 - 使用 向量 + 双竖线 的方式表示 向量长度(Vector Length),如:\(|\vec{a}|\)。
单位向量可以通过向量除以向量长度的方式计算得到,如下所示。
\[\begin{aligned} \widehat{a} = \vec{a} / |\vec{a}| \end{aligned}\]在计算机图形学中,单位向量的应用非常多,比如:法线向量。在计算光线的折射和反射时,法线必不可少。
向量的加减运算
向量的加减运算可以使用 平行四边形法则 或 三角形法则 进行计算,如下图所示。
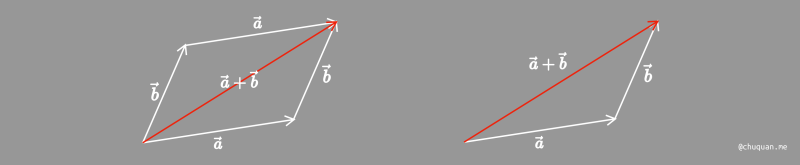
向量的加减运算非常简单,只需要把两个向量的对应坐标的值进行加减运算即可,如下所示。
\[\begin{aligned} \vec{a} + \vec{b} = \left( \begin{matrix} a_x & a_y \end{matrix} \right) + \left( \begin{matrix} b_x & b_y \end{matrix} \right) = \left( \begin{matrix} a_x + b_x & a_y + b_y \end{matrix} \right) \\ \vec{a} - \vec{b} = \left( \begin{matrix} a_x & a_y \end{matrix} \right) - \left( \begin{matrix} b_x & b_y \end{matrix} \right) = \left( \begin{matrix} a_x - b_x & a_y - b_y \end{matrix} \right) \end{aligned}\]向量的乘法运算
向量的乘法运算比较特殊,它有两种乘法运算,分别是:
- 点积(Dot Product),或称 点乘
- 叉积(Cross Product),或称 叉乘
点积
两个向量之间的点积是一个数值,一般使用 点运算符 表示。
点积的运算非常简单,只要将每个向量对应的坐标值相乘并求和即可,如下所示为一个点积的示例。
\[\begin{aligned} \vec{a} \cdot \vec{b} = \left( \begin{matrix} a_x & a_y & a_z \end{matrix} \right) \left( \begin{matrix} b_x \\ b_y \\ b_z \\ \end{matrix} \right) = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z \end{aligned}\]向量点积的特性
- 符合交换律,即 \(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\)
- 符合分配律,即 \(\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}\)
- 不符合结合律。点乘的结果是一个标量,不是向量,因此无法与另一个向量继续进行点乘运算。
在计算机图形学中,点积的应用非常广泛,主要包括:
- 计算两个向量之间的夹角
- 计算一个向量在另一个向量上的投影
- 计算一个向量正交分解后的两个向量
- 判断一个向量相对于另一个向量是正向还是反向
下面,我们来看一下这几种应用是如果通过计算实现的。
首先,如何计算两个向量之间的夹角?在几何上,两个向量的点积与它们的长度以及它们之间的夹角 \(a\) 有关,确切的公式巧妙地将线性代数和三角函数联系在了一起,如下所示。
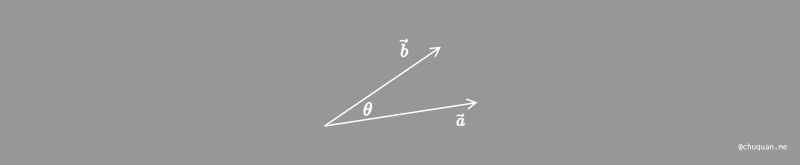
其次,如何计算一个向量在另一个向量上的投影?如下所示,求向量 \(\vec{b}\) 在向量 \(\vec{a}\) 上的投影 \(\vec{b}_\bot\),很显然,\(\vec{b}_\bot\) 与 \(\vec{a}\) 的方向是一致的,只是长度可能不同。因此,我们可以通过前面提到的方式计算两者之间的夹角,然后计算投影长度,并使用该长度乘以单位向量 \(\widehat{a}\) 即可。

接着,如何计算一个向量正交分解后的两个向量?上面我们在计算一个向量在另一个向量上的投影时,已经计算得到了一个方向的分解向量,另一个方向的分解向量我们只需通过向量减法即可得到,如下所示。
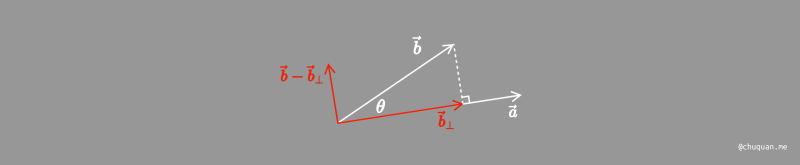
最后,如何判断一个向量相对于另一个向量是正向还是反向?判断两个向量的方向关系,本质上是看两者之间的夹角,如果是锐角,则认为是正向,如果是钝角,则认为是反向,如下所示。
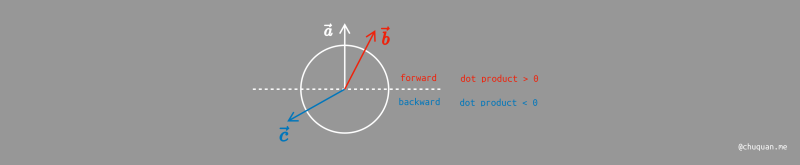
叉积
两个向量之间的叉积是一个向量,一般使用 叉乘符号 表示。
叉积是一个垂直于两个向量的向量,其方向可以通过 右手螺旋定则 确定。
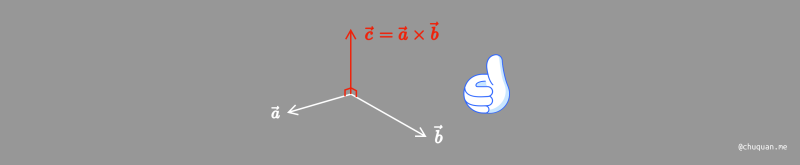
向量叉积的特性
- 符合分配律,即 \(\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\)
- 不符合结合律,即 \((\vec{a} \times \vec{b}) \times \vec{c} \neq \vec{a} \times (\vec{b} \times \vec{c})\)
- 不符合交换律,即 \(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)
在计算机图形学中,乘积的应用主要包括一下这些:
- 判断一个向量相对于另一个向量的左右关系
- 判断一个向量相对于一个三角形的内外关系
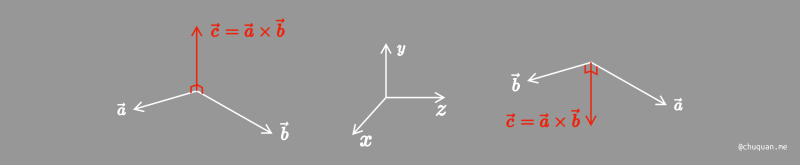
那么,如何判断一个向量相对于另一个向量的左右关系?可以直接判断两个向量叉积的正负值。如下所示,在一个 3D 坐标中,\(\vec{a}\) 和 \(\vec{b}\) 的叉乘符合右手螺旋定则的方向(图中与 Y 轴方向相同),则表示 \(\vec{A}\) 在 \(\vec{B}\) 的右边,反之则表示 \(\vec{A}\) 在 \(\vec{B}\) 的左边。
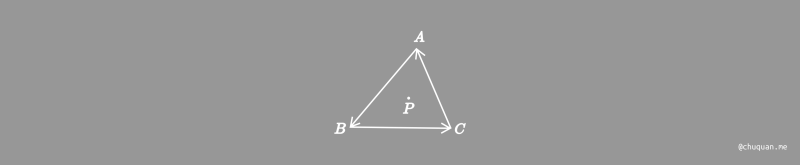
以及,如何判断一个向量相对于一个三角形的内外关系?事实上,我们可以利用上面这种左右关系判断的方法来组合判断。如下所示,我们可以分别判断 \(\overrightarrow{AP}\) 和 \(\overrightarrow{AB}\) 的左右关系,\(\overrightarrow{BP}\) 和 \(\overrightarrow{BC}\) 的左右关系,\(\overrightarrow{CP}\) 和 \(\overrightarrow{CA}\) 的左右关系,如果前者都在后者的一边(左边或右边),那么 \(P\) 就在三角形内;否则,在三角形外。
矩阵
矩阵是一个 \(m\) 行 \(n\) 列的数字阵列,通常我们使用一个 加粗的大写字母 抽象表示一个矩阵。在计算机图形学中,它被广泛应用于各种变换计算中,比如:平移、旋转、缩放等。
矩阵的乘法运算
矩阵的乘法必须满足一个前提:矩阵 \(A\) 的列数等于矩阵 \(B\) 的行数,即
(M x N)(N x P) = (M x P)。
矩阵 \(A\) 乘以矩阵 \(B\) 得到矩阵 \(C\),其中矩阵 \(C\) 中的任意元素 (i, j)
的值等于 \(A\) 中第 i 行与
\(B\) 中第 j
列的点积,如下所示是一个矩阵乘法的示例。
矩阵乘法的特性
- 不符合交换律,即 \(AB \neq BA\)
- 符合分配律,即 \(A(B + C) = AB + BA\)
- 符合结合律,即 \((AB)C = A(BC)\)
在计算机图形学中,向量也会使用矩阵(行矩阵或列矩阵)来表示,向量之间的乘法以及向量与矩阵的乘法都符合矩阵乘法的基本规则。
矩阵的转置运算
矩阵的转置本质上就是沿着主对角线(从左上角至右下角)的对角线将 i x j 的矩阵翻转成 j x i 的矩阵。一般我们使用一个 上标 T 表示一个矩阵的转置,如:\(A^T\)。
如下所示,是一个矩阵转置运算的示例。
\[\begin{aligned} \left( \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{matrix} \right)^T = \left( \begin{matrix} 1 & 3 & 5 \\ 2 & 4 & 6 \\ \end{matrix} \right) \end{aligned}\]矩阵转置的特性
- \((AB)^T = B^TA^T\)
矩阵的类型
下面,我们来介绍各种不同类型的矩阵。
对角矩阵
对角矩阵,其主对角线(从左上角到右下角)上的元素都是非 0,其他元素都为 0。
单位矩阵
单位矩阵,其主对角线(从左上角到右下角)上的元素都为 1,其余元素都为 0,一般使用大写字母 \(I\) 来表示。单位矩阵是一个特殊的对角矩阵。如下所示,是一个单位矩阵实例。
\[\begin{aligned} I_{3 \times 3} = \left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right) \end{aligned}\]逆矩阵
给定一个矩阵 \(A\),如果存在一个与之维度相同的矩阵,使得这两个矩阵相乘的结果是一个单位矩阵,那么我们称这个矩阵为矩阵 \(A\) 的逆矩阵,使用 \(A^{-1}\) 表示。如下所示,为逆矩阵的示例。
\[\begin{aligned} A A^{-1} =& A^{-1}A = I \\ (AB)^{-1} =& B^{-1}A^{-1} \end{aligned}\]矩阵的应用
上述我们介绍的向量的两种运算,其实完全可以使用矩阵的乘法来实现。
关于向量的点积,我们可以使用如下矩阵乘法来表示。
\[\begin{aligned} \vec{a} \cdot \vec{b} = \vec{a}^T \cdot \vec{b} = \left( \begin{matrix} a_x & a_y & a_z \end{matrix} \right) \left( \begin{matrix} b_x \\ b_y \\ b_z \\ \end{matrix} \right) = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z \end{aligned}\]关于向量的叉积,我们可以使用如下矩阵乘法来表示,如下所示。其中 \(A^*\) 为矩阵 \(A\) 的对偶矩阵。
\[\begin{aligned} \vec{a} \times \vec{b} = A^* b = \left( \begin{matrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \\ \end{matrix} \right) \left( \begin{matrix} b_x \\ b_y \\ b_z \\ \end{matrix} \right) = \left( \begin{matrix} a_y \cdot b_z - a_z \cdot b_y \\ a_z \cdot b_x - a_x \cdot b_z \\ a_x \cdot b_y - a_y \cdot b_x \\ \end{matrix} \right) \end{aligned}\]总结
本文介绍了点、向量、矩阵的基本定义和运算方法。向量的乘法包含两种:点积和叉积,两者被广泛应用在了在计算机图形学中。
点积和叉积的具体运算可以通过矩阵运算来实现,这也是为什么我们常说计算机图形学中包含了大量矩阵运算。
下文,我们将探讨矩阵在图形的变换中的应用,敬请期待吧~
参考
- 《GAMES 101》
- 《计算机图形学入门:3D渲染指南》
- 史上最全Markdown公式、符号总结
