Paul Heckel 差分算法

发表于 更新于 分类于 Waline：

前一篇 文章 我们介绍了 Myers 差分算法，其主要应用在版本控制系统，用于比较不同版本的源代码，比如：git、svn、gerrit 等。本文，我们再来介绍一下 UI 框架中常用于数据差异检测的算法——Paul Heckel 差分算法。

解决什么问题？

通过前一篇文章，我们知道 Myers 差分算法主要用于 解决特定设定下的最小编辑距离问题，即：当编辑操作只支持 插入 和 删除 时，计算一个文件从 A 状态转换成 B 状态所需的最少编辑次数（或编辑方式）。算法特别适用于对编辑次数敏感，但是对速度和内存不敏感的系统，比如版本控制系统。

对比而言，Paul Heckel 差分算法则主要用于 解决最小化差异问题，即：当一个文件从 A 状态转换成 B 状态时，两种状态之间的数据差异。算法会为每一项差异定义一个对应的类型（操作），比如：删除、插入、移动等，其侧重点在于最小化差异，而不是最小化编辑。Paul Heckel 差分算法特别适合对计算速度敏感，但是对于 差异不敏感 的系统，比如实时数据分析系统，UI 框架数据差分。

算法原理

核心思想

Paul Heckel 算法使用三种类型来表示两个文件之间的差异结果，分别是：删除、插入、移动。基于此，算法的核心思路其实非常简单，分别是：

  • 确定旧文件中待删除的行
  • 确定新文件中待插入的行
  • 确定旧文件至新文件中待移动的行，并记录行号关系（旧文件行号、新文件行号）

数据结构

很显然，根据算法的核心思想，新旧两个文件中的所有行最终都将被分类为三种类型（如果行的内容和位置都没有变化，则分类为移动类型，只不过移动的行号保持不变而已）。

Paul Heckel 差分算法使用两个数组 NA（New Array）和 OA（Old Array）分别记录新旧两个文件的每一行的信息。数组元素分为两种类型：指针 或 行号。通过这种方式，我们可以对新旧两个文件中的所有行进行分类：

  • 当旧文件中某一行在 OA 中对应的元素为指针时，表示这一行是待删除的。
  • 当新文件中某一行在 NA 中对应的元素为指针时，表示这一行是待插入的。
  • 当新文件（旧文件）中某一行在 NA（OA）中对应的元素为行号时，表示这一行是待移动的。行号记录了它在旧文件（新文件）的位置。两两配对。

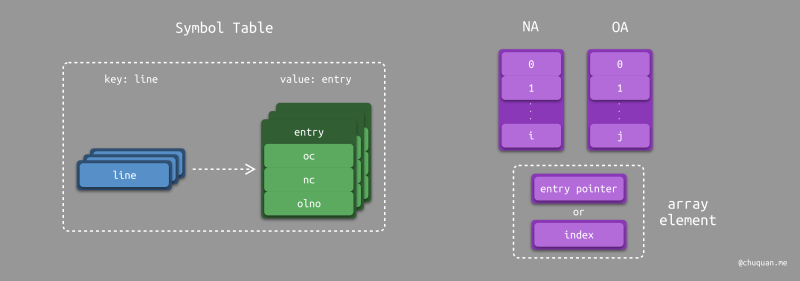
这里提到了数组元素可能是指针类型，那么它到底指向什么类型的数据呢？事实上，这是 Paul Heckel 算法预定义的一种数据类型，这里我们称之为 entry 类型。entry 的定义如下所示：

1
2
3
4
5
struct entry {
    int oc;         // old count. 记录该行在旧文件中出现的次数
    int nc;         // new count. 记录该行在新文件中出现的次数
    int olno;       // old line number. 记录该行在旧文件中的位置
}

同时，为了方便快速查找某一行所对应的 entry，这里还定义了一个哈希表，算法中称为 符号表（Symbol Table），其中 Key 为行内容，Value 为 entry。

如下所示，为算法所定义的相关数据结构。

算法实现

算法的实现主要分为三个部分，分别是：

  • 构建阶段
  • 移动类型筛选
  • 分析输出

下面依次进行介绍。

构建阶段

在构建阶段，将遍历新文件和旧文件的每一行，同时构建数组、符号表表项（Key 为行内容，Value 为 Entry）。

  • 对于新文件，在构建 Entry 时，对 nc 字段加 1。
  • 对于旧文件，在构建 Entry 时，对 oc 字段加 1，并设置 olno 为当前的行号。

在构建数组（ NA 和 OA ）时，其元素均为指针类型，指向当前行对应在符号表中的 entry。

很显然，构建阶段需要进行两次遍历，其对应在论文中分别是 Pass 1 和 Pass 2。

移动类型筛选

在构建阶段完成后，数组 NA 和 OA 中的所有元素都是指针类型，指向符号表中的某个 entry。接下来，只要我们把属于 移动 类型的行筛选出来，也就是把数组中的某些元素修改为行号，即可完成对三种类型的分类。

在继续介绍之前，我们先说明一种常见的情况：一个文件中行内容可能是唯一项，也可能是重复项。比如，在下图所示的两个文件中，THE 在新旧两个文件中都重复出现了两次，A、MASS、OF 等内容在各自的文件中都是唯一项。对此，算法的处理方式也有所不同。

唯一项筛选

对于唯一项，很显然，如果符合移动类型的话，行所对应的 entry 中的 oc 和 nc 的值均为 1，表示它们在新旧文件中各自只出现了一次。

由于移动类型是对等的，所以我们只需要遍历 NA 数组就可以找到所有唯一项的移动类型。具体的做法是：

  • 遍历 NA 数组，根据元素（指针类型）找到对应的 entry。
  • 判断 entry 的 oc 和 nc 字段是否均为 1。
    • 如果符合条件，则将 NA 对应的位置的元素设置成行号类型，值为 olno（即该行对应在旧文件中的位置）；同时将 OA 的 olno 位置的元素设置成行号类型，值为 i（即当前遍历到的行号）。此时，两者实现了移动匹配（各自记录了彼此的位置）。
    • 如果不符合条件，则将继续遍历 NA。

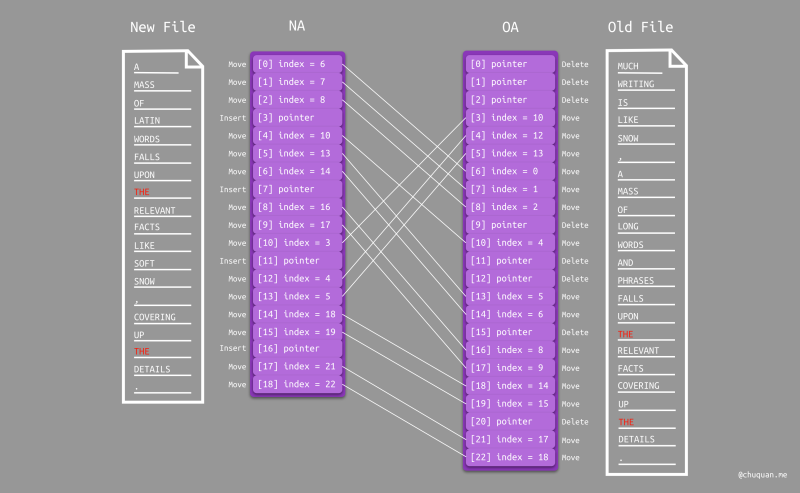
在遍历完成后，数组 NA 和 OA 中均可能有一部分元素变成了行号类型，值为对方的某个行号。本轮遍历对应在论文中是 Pass 3。

重复项筛选

对于重复项，算法采用了一种模糊处理的方式。这里主要遵循了下面这个设定：

If a line has been found to be unaltered, and the lines immediately adjacent to it in both files are identical, then these lines must be the same line. This information can be used to find blocks of unchanged lines.

译：如果某一行没有发生改变，并且在新旧两个文件中与它紧邻的行都是相同的，那么这些行必须是相同的行。这个信息可以用来找到未改变的行块。

上述设定需要寻找某一行前后邻近的行，很显然，需要进行两次遍历，分别是正向遍历和反向遍历。同样，这里只需要遍历 NA 即可。

对于正向遍历，会进行以下处理：

  • 判断 NA[i] 是否指向 OA[j]（当 NA[i] 的元素为行号时，且行号为 j，即表示 NA[i] 指向 OA[j]）
    • 如果是，则表示当前行是已发现的属于 移动 类型的行，那么继续判断 NA[i+1] 是否与 OA[j+1] 指向同一个 entry。
      • 如果是，则将 NA[i+1] 的元素设置成行号类型，值为 j+1；将 OA[j+1] 的元素设置成行号类型，值为 i+1。
  • 此外其他情况均继续遍历 NA。

对于反向遍历，其处理与正向遍历类似，只不过方向相反：

  • 判断 NA[i] 是否指向 OA[j]（当 NA[i] 的元素为行号时，且行号为 j，即表示 NA[i] 指向 OA[j]）
    • 如果是，则表示当前行是已发现的属于 移动 类型的行，那么继续判断 NA[i-1] 是否与 OA[j-1] 指向同一个 entry。
      • 如果是，则将 NA[i-1] 的元素设置成行号类型，值为 j-1；将 OA[j-1] 的元素设置成行号类型，值为 i-1。
  • 此外其他情况均继续遍历 NA。

经过这一番操作后，算法会处理筛选出重复项，下图所示红色标识。这些重复项的 移动 类型，可以与某些唯一项连成 移动块。

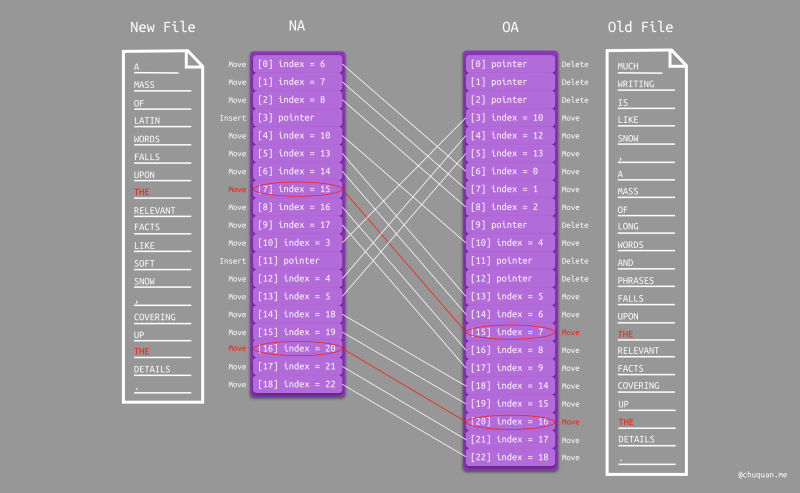
重复项的筛选，经历了两次遍历，分别对应论文中的 Pass 4 和 Pass 5。

分析输出

经过上述一系列处理之后，数组 NA 和 OA 将所有行分成了三种类型，分别是 删除、插入、移动。根据这些信息，我们可以遍历 NA 和 OA，输出差异的分析结果。这一步，对应在论文中则是 Pass 6。

算法缺陷

至此，仔细的同学可能会发现，在重复项筛选的过程中，算法会遗漏一部分属于 移动 类型的行，而将它们误判为 删除 或 插入 类型。

如下所示为算法误判的一个例子。我们将新文件中的第一个 THE 前后相邻的两个行改成两个唯一项 UNIQUE1 和 UNIQUE2。由于旧文件中不存在 UNIQUE1 和 UNIQUE2，所以它们是属于插入类型的项。此时，我们再看上述 Pass 4 和 Pass 5 的执行逻辑，可以看出新文件中的第一个 THE 并不会并筛选为移动类型，而是被错误地认为是插入类型。所以说，Paul Heckel 算法对于重复项的处理采用了一种模糊处理的方式。

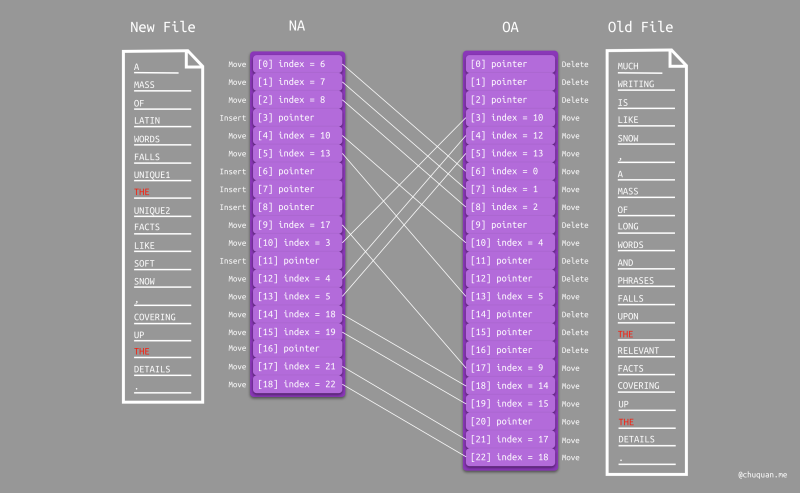
事实上，这也是 Paul Heckel 差分算法的特点，它牺牲了一部分差异精准度，换来了更快的分析速度。这也是为什么我们在「解决了什么问题」这一节中说 Paul Heckel 算法适合速度敏感、差异不敏感的系统。

算法应用

基于 Paul Heckel 算法变种的差分算法应用其实非常多，在 iOS 开发中就有很多相关的框架，比如：IGListKit、DifferenceKit、RxDataSources、FlexibleDiff、DeepDiff 等。下面，我们来看看 IGListKit 是如何应用并优化 Paul Heckel 差分算法的。

类型扩展

由于绝大多数应用都对 Paul Heckel 算法进行了一定程度的优化，因此，我们必须要先了解它们到底优化了什么。

事实上，原始的 Paul Heckel 算法只对 位置 和 内容 两个维度进行差分检测（符号表的 Key 和数据判等都是基于 内容），从而产生 3 种分类，如下表所示。

位置 内容 分类
相同 相同 move（起始位置不变）
相同 不同 insert/delete
不同 相同 move
不同 不同 insert/delete

但是在实际应用中，为了支持更加复杂多变的场景，一般会额外支持 标识 或 ID 的维度。此时，算法将基于 标识、位置、内容 三个维度进行差分检测（符号表的 Key 基于 标识，数据判等基于 内容），对此将产生 4 种分类，如下表所示。

标识（ID） 位置 内容 分类
相同 相同 相同 move（起始位置不变）
相同 相同 不同 update
相同 不同 相同 move
相同 不同 不同 update & move
不同 相同 相同 insert/delete
不同 相同 不同 insert/delete
不同 不同 相同 insert/delete
不同 不同 不同 insert/delete

IGListDiff

数据结构

在数据结构定义上，IGListDiff 与原始算法类似，也定义了一个符号表和两个数组，如下图所示。

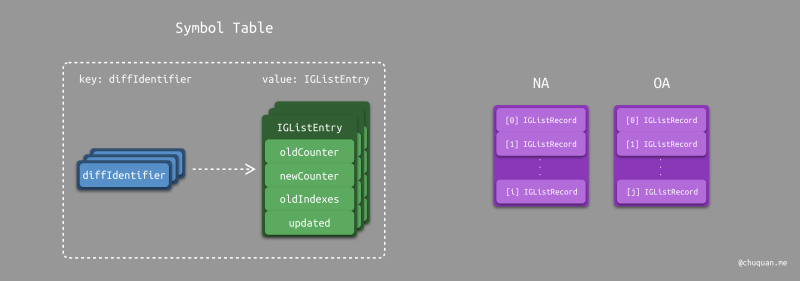
对于符号表，IGListDiff 使用数据的标识（ID）作为 Key，以 IGListEntry 作为 Value。IGListEntry 的定义如下所示，很显然，它与原始算法中的 entry 结构非常类似：

  • oldCounter 和 newCounter 对应的是 oc 和 nc 字段。
  • oldIndex 对应 olno，但是它支持记录多个位置信息，支持处理重复项。olno 只能记录一个位置。
  • IGListEntry 额外还有一个 updated 字段，用于标记扩展的 更新（update）类型。
1
2
3
4
5
6
7
8
9
10
11
/// Used to track data stats while diffing.
struct IGListEntry {
    /// The number of times the data occurs in the old array
    NSInteger oldCounter = 0;
    /// The number of times the data occurs in the new array
    NSInteger newCounter = 0;
    /// The indexes of the data in the old array
    stack<NSInteger> oldIndexes;
    /// Flag marking if the data has been updated between arrays by checking the isEqual: method
    BOOL updated = NO;
};

对于两个数组，IGListDiff 同样具备，区别在于元素的表示形式。在原始算法中，NA 和 OA 数组存储的元素可能是指针或行号，而 IGListDiff 则使用 IGListRecord 类型来记录两种信息，其定义如下所示。其中，entry 用于存储指针，index 用于存储行号。

1
2
3
4
5
6
7
8
9
10
/// Track both the entry and algorithm index. Default the index to NSNotFound
struct IGListRecord {
    IGListEntry *entry;
    mutable NSInteger index;

    IGListRecord() {
        entry = NULL;
        index = NSNotFound;
    }
};

除此之外，IGListDiff 定义一个 IGListDiffable 协议，所有希望调用 IGListDiff 差分算法的数据都必须支持该协议。如下所示为 IGListDiffable 的定义。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
NS_SWIFT_NAME(ListDiffable)
@protocol IGListDiffable

/**
 Returns a key that uniquely identifies the object.
 @return A key that can be used to uniquely identify the object.
 @note Two objects may share the same identifier, but are not equal. A common pattern is to use the `NSObject` category for automatic conformance. However this means that objects will be identified on their pointer value so finding updates becomes impossible.
 @warning This value should never be mutated.
 */
- (nonnull id<NSObject>)diffIdentifier;

/**
 Returns whether the receiver and a given object are equal.
 @param object The object to be compared to the receiver.
 @return `YES` if the receiver and object are equal, otherwise `NO`.
 */
- (BOOL)isEqualToDiffableObject:(nullable id<IGListDiffable>)object;

@end

算法会使用数据的 diffIdentifier 作为标识（ID），符号表也将以此为 Key 记录对应的 entry。另一个协议方法 isEqualToDiffableObject: 则用于进行内容判等。

关于输出，原始算法并没有做相关说明。对此，IGListDiff 自定义了两种输出结构，分别是 IGListIndexSetResult 和 IGListIndexPathResult，如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
NS_SWIFT_NAME(ListIndexPathResult)
@interface IGListIndexPathResult : NSObject
// The index paths inserted into the new collection.
@property (nonatomic, copy, readonly) NSArray<NSIndexPath *> *inserts;
// The index paths deleted from the old collection.
@property (nonatomic, copy, readonly) NSArray<NSIndexPath *> *deletes;
// The index paths in the old collection that need updated.
@property (nonatomic, copy, readonly) NSArray<NSIndexPath *> *updates;
// The moves from an index path in the old collection to an index path in the new collection.
@property (nonatomic, copy, readonly) NSArray<IGListMoveIndexPath *> *moves;
// A Read-only boolean that indicates whether the result has any changes or not. `YES` if the result has changes, `NO` otherwise.
@property (nonatomic, assign, readonly) BOOL hasChanges;
@end


NS_SWIFT_NAME(ListIndexSetResult)
@interface IGListIndexSetResult : NSObject
// The indexes inserted into the new collection.
@property (nonatomic, strong, readonly) NSIndexSet *inserts;
// The indexes deleted from the old collection.
@property (nonatomic, strong, readonly) NSIndexSet *deletes;
// The indexes in the old collection that need updated.
@property (nonatomic, strong, readonly) NSIndexSet *updates;
// The moves from an index in the old collection to an index in the new collection.
@property (nonatomic, copy, readonly) NSArray<IGListMoveIndex *> *moves;
// A Read-only boolean that indicates whether the result has any changes or not. `YES` if the result has changes, `NO` otherwise.
@property (nonatomic, assign, readonly) BOOL hasChanges;
@end

两者均携带了所有差异数据的位置信息，包括：插入、删除、更新、移动。区别则在于 IGListIndexPathResult 用于表示位置信息的类型是 NSIndexPath 类型，适用于 iOS 中的列表数据，IGListIndexSetResult 用于表示位置信息的类型是 NSInteger 类型，更适合通用的数组数据。

核心逻辑

IGListDiff 中 IGListDiff.m 文件的 IGListDiffing 方法实现了差分算法的核心逻辑，大概可分为三个步骤：

  • 构建阶段
  • 标记移动类型和更新类型
  • 格式化输出

构建阶段

在构建阶段，IGListDiff 分别正向遍历新数据和反向遍历旧数据，从而构建数组元素 NA、OA、符号表，这一点与原始算法类似。这里反向遍历旧数据是因为这里使用栈来记录所有的 olno，以便后续正向地出栈旧数据的位置信息。具体代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
unordered_map<id<NSObject>, IGListEntry, IGListHashID, IGListEqualID> table;

// pass 1
// create an entry for every item in the new array
// increment its new count for each occurence
vector<IGListRecord> newResultsArray(newCount);
for (NSInteger i = 0; i < newCount; i++) {
    id<NSObject> key = IGListTableKey(newArray[i]);
    IGListEntry &entry = table[key];
    entry.newCounter++;

    // add NSNotFound for each occurence of the item in the new array
    entry.oldIndexes.push(NSNotFound);

    // note: the entry is just a pointer to the entry which is stack-allocated in the table
    newResultsArray[i].entry = &entry;
}

// pass 2
// update or create an entry for every item in the old array
// increment its old count for each occurence
// record the original index of the item in the old array
// MUST be done in descending order to respect the oldIndexes stack construction
vector<IGListRecord> oldResultsArray(oldCount);
for (NSInteger i = oldCount - 1; i >= 0; i--) {
    id<NSObject> key = IGListTableKey(oldArray[i]);
    IGListEntry &entry = table[key];
    entry.oldCounter++;

    // push the original indices where the item occurred onto the index stack
    entry.oldIndexes.push(i);

    // note: the entry is just a pointer to the entry which is stack-allocated in the table
    oldResultsArray[i].entry = &entry;
}

标记移动类型和更新类型

构建完成之后，开始对移动类型和更新类型进行标记，具体如下代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// pass 3
// handle data that occurs in both arrays
for (NSInteger i = 0; i < newCount; i++) {
    IGListEntry *entry = newResultsArray[i].entry;

    // grab and pop the top original index. if the item was inserted this will be NSNotFound
    NSCAssert(!entry->oldIndexes.empty(), @"Old indexes is empty while iterating new item %li. Should have NSNotFound", (long)i);
    const NSInteger originalIndex = entry->oldIndexes.top();
    entry->oldIndexes.pop();

    // originalIndex 存在表示「标识相同」。这里判断 originalIndex < oldCount 应该是为了做越界保护。
    if (originalIndex < oldCount) {
        // 对于「内容不同」的项，将其标记为更新类型
        const id<IGListDiffable> n = newArray[i];
        const id<IGListDiffable> o = oldArray[originalIndex];
        switch (option) {
            case IGListDiffPointerPersonality:
                // 基于指针判断
                if (n != o) {
                    // 如果指针不同，则表示更新类型
                    entry->updated = YES;
                }
                break;
            case IGListDiffEquality:
                // 基于指针 + 内容判断
                if (n != o && ![n isEqualToDiffableObject:o]) {
                    // 如果指针不同，并且内容不同，则表示更新类型
                    entry->updated = YES;
                }
                break;
        }
    }
    // newCounter > 0 && oldCounter > 0 表示新旧数据均存在
    // originalIndex != NSNotFound 的是为了让新旧数据两两匹配，因为 oldIndexes 随着遍历的迭代，始终在出栈。
    if (originalIndex != NSNotFound
        && entry->newCounter > 0
        && entry->oldCounter > 0) { 
        // 对于「内容相同」的项，交换记录其在对方数组中的位置，表示移动类型
        newResultsArray[i].index = originalIndex;
        oldResultsArray[originalIndex].index = i;
    }
}

从上述代码中可以看出，每次迭代会从根据 NA 数组元素 IGListRecord 的 entry 字段索引到符号表中对应的 IGListEntry。然后从 IGListEntry 的 oldIndexes 字段出栈一个旧文件中存在的位置。

如果 originalIndex 存在，则表示 NA 和 OA 均存在，此时进一步判断内容，如果内容发生了变化则标记 updated 字段为 YES。判断内容变化的方式有两种，用户可以选择配置：

  • 基于指针判断：如果指针不同，则表示数据发生了变化
  • 基于指针+内容判断：如果指针不同，并且内容不同，则表示数据发生了变化

在遍历过程中，还会记录移动类型的位置信息。它的前提条件包含两部分：

  • newCounter > 0 && oldCounter > 0：表示新旧数据均存在
  • originalIndex != NSNotFound：表示新旧数据可以进行移动类型的匹配，每一次匹配，oldIndexes 都会出栈一次，消耗一次对等的匹配。举个例子：
    • 如果 newCounter = 3，oldCounter = 2 时，NA 中第三个数据会被归为插入类型，前两个数据会被归为移动类型。
    • 如果 newCounter = 2，oldCounter = 3 时，OA 中的第三个数据会被归为删除类型，前两个数据会被归为移动类型。

格式化输出

首先，遍历 OA 数组，确定删除类型，具体代码如下所示。数组元素的 index 类型为 NSNotFound 类似于原始算法中 OA 元素的类型为指针。当符合这个条件时，表示数据类型为删除类型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// iterate old array records checking for deletes
// incremement offset for each delete
for (NSInteger i = 0; i < oldCount; i++) {
    deleteOffsets[i] = runningOffset;
    const IGListRecord record = oldResultsArray[i];
    // if the record index in the new array doesn't exist, its a delete
    // 对 OA 中的删除项进行分类
    if (record.index == NSNotFound) {
        addIndexToCollection(returnIndexPaths, mDeletes, fromSection, i);
        runningOffset++;
    }

    addIndexToMap(returnIndexPaths, fromSection, i, oldArray[i], oldMap);
}

其次，遍历 NA 数组，确定插入、更新、移动等类型，具体代码如下所示。数组元素的 index 类型为 NSNotFound 类似于原始算法中 NA 元素的类型为指针。当符合这个条件时，表示数据类型为插入类型。否则，均属于移动类型。

这里由于 IGListDiff 额外扩展了一个 updated 字段，所以有一部分元素为同时标记为更新类型。这一点其实很容易理解，当新旧数据中有一个数据标识相同，但是位置不同，且内容不同，我们可以认为它做了一次移动操作修改了位置，又做了一次更新操作修改了内容。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
for (NSInteger i = 0; i < newCount; i++) {
    insertOffsets[i] = runningOffset;
    const IGListRecord record = newResultsArray[i];
    const NSInteger oldIndex = record.index;
    // add to inserts if the opposing index is NSNotFound
    if (record.index == NSNotFound) {
        // 确定插入类型
        addIndexToCollection(returnIndexPaths, mInserts, toSection, i);
        runningOffset++;
    } else {
        // note that an entry can be updated /and/ moved
        if (record.entry->updated) {
            // 确定更新类型
            addIndexToCollection(returnIndexPaths, mUpdates, fromSection, oldIndex);
        }

        // calculate the offset and determine if there was a move
        // if the indexes match, ignore the index
        // 确定移动类型
        const NSInteger insertOffset = insertOffsets[i];
        const NSInteger deleteOffset = deleteOffsets[oldIndex];
        if ((oldIndex - deleteOffset + insertOffset) != i) {
            id move;
            if (returnIndexPaths) {
                NSIndexPath *from = [NSIndexPath indexPathForItem:oldIndex inSection:fromSection];
                NSIndexPath *to = [NSIndexPath indexPathForItem:i inSection:toSection];
                move = [[IGListMoveIndexPath alloc] initWithFrom:from to:to];
            } else {
                move = [[IGListMoveIndex alloc] initWithFrom:oldIndex to:i];
            }
            [mMoves addObject:move];
        }
    }

    addIndexToMap(returnIndexPaths, toSection, i, newArray[i], newMap);
}

优化小结

整体而言，IGListDiff 在 Paul Heckel 差分算法的基础上扩展了差分类型，从原来的 插入、删除、移动 3 种类型扩展成 插入、删除、移动、更新 4 种类型。类型的扩展本质上是通过增加检测维度实现的，Paul Heckel 差分算法只支持 位置、内容 2 个维度进行检测，而 IGListDiff 则支持 标识、位置、内容 3 个维度进行检测。

此外，IGListDiff 实现了精准检测，而 Paul Heckel 算法实现的是模糊处理，会存在移动类型误判为插入或删除等情况。这种精准检测的能力，适用于对差异敏感的系统，使得算法的应用场景进一步扩大。

总结

本文首先介绍了原始的 Paul Heckel 差分算法的实现原理。原始的 Paul Heckel 差分算法基于位置、内容 2 个维度进行差分检测，支持检测插入、删除、移动等 3 种类型。但是，其实现的是一种模糊处理的差分检测，会存在将移动类型归为插入或删除的情况。

其次，我们介绍了 IGListKit 中的 IGListDiff 模块，其在 Paul Heckel 差分算法的基础上进行了优化，基于标识、位置、内容 3 个维度进行差分检测，支持检测插入、删除、移动、更新等 4 种类型。IGListDiff 实现了一种精确分析的差分算法，这更符合我们在 UI 框架中对于数据差异精准检测的需求。

通过上文的介绍，我们可以举一反三猜想地其他应用是如何实现数据差分检测的。对此，如果你感兴趣的话，可以研究一个其他的框架，来印证一下你的猜想，甚至可以考虑自己实现差分算法。

参考

  1. A Technique for Isolating Differences Between Files. Paul Heckel.
  2. Isolating Differences Between Files
  3. IGListKit