计算机图形学基础(7)——辐射度量学
在介绍光线追踪之前,我们先来学习一下其所涉及的重要内容——辐射度量学。由于该内容相对独立,这里单开一篇文章来进行介绍。
概述
本质上,辐射度量学是在物理层面准确定义光照的方法。在 《计算机图形学基础(5)——着色》 一文中我们提到了光照强度,我们将半径为 \(r\) 时,对应的球面的一个点的光照强度为 \(I\),那么具体它的单位是什么呢?在了解辐射度量学之后,这个疑问就能得到解答。
在辐射度量学中涉及了很多相关术语,这里我将它们分为两部分进行介绍。
几何
首先我们来看几何的相关术语,主要包含以下几个:
- 角(Angles)
- 立体角(Solid Angles)
- 微分立体角(Differential Solid Angles)
角
在平面几何中,角的定义是弧长与半径的比值,其中 \(\theta\) 表示角,\(l\) 表示弧长,\(r\) 表示圆的半径,如下所示。圆自身的角度为 \(2\pi\)。
\[\begin{aligned} \theta = \frac{l}{r} \end{aligned}\]
立体角
在立体几何中,立体角的定义则是弧面积与半径平方的比值,其中 \(\Omega\) 表示立体角,\(A\) 表示弧面积,\(r\) 表示球的半径,如下所示。球自身的立体角为 \(4\pi\)。立体角主要用于描述空间中的一个锥体的张开角度。
\[\begin{aligned} \Omega = \frac{A}{r^2} \end{aligned}\]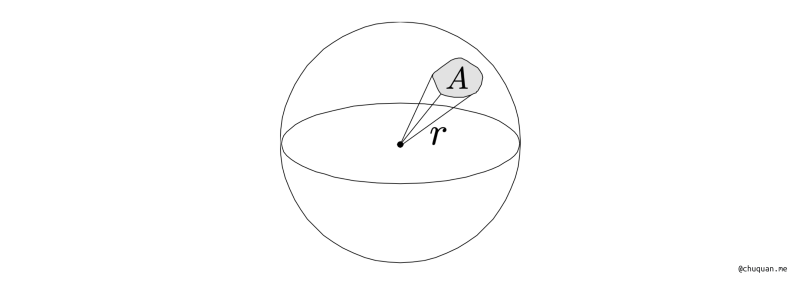
微分立体角
微分立体角通过两个角度来定义球面上的一个唯一的方向,如下所示。其中,两个角度分别是:
- 与 \(z\) 轴形成的夹角 \(\theta\)
- 绕 \(z\) 轴形成的夹角 \(\phi\)
计算微分立体角,我们首先两个角度在球面所形成方向所占据的单位面积 \(dA\)。按照微分的思想,我们认为该面积等同于矩形的面积,因此我们要计算它的长和宽,分别为 \(rsin{\theta}d\phi\) 和 \(rd\theta\),由此可以计算该单位面积。从而进一步求解微分立体角 \(d\omega\),如下所示。
\[\begin{aligned} dA = & (r d\theta)(r sin{\theta} d\phi) = r^2 sin\theta d\theta d\phi \\ d\omega = & \frac{dA}{r^2} = sin\theta d\theta d\phi \end{aligned}\]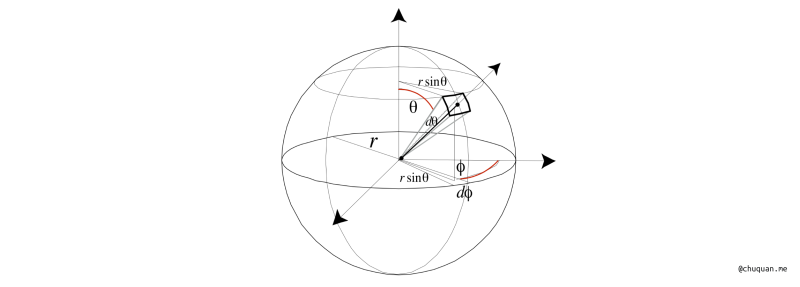
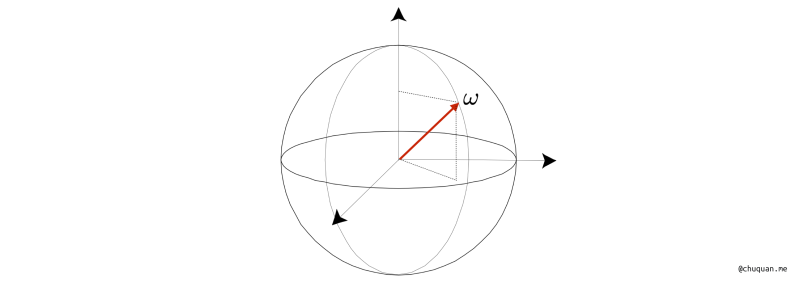
在辐射度量学中,我们通常用 \(\omega\) 来表示三维空间中的一个方向。我们可以使用 \(\theta\) 和 \(\phi\) 来确定其方向,并且还可以结合 \(d\theta\) 和 \(d\phi\) 来计算其微分立体角。
光学物理
在辐射度量学中,主要涉及以下几个光学物理相关术语。
- 辐射能量(Radiant Energy)
- 辐射通量(Radiant Flux)
- 辐射强度(Radiant Intensity)
- 辐射照度(Irradiance)
- 辐射亮度(Radiance)
辐射能量
辐射能量(Radiant Energy)表示电磁辐射的能量,用符号 \(Q\) 表示,以 焦耳(J = Joule)为单位。
\[\begin{aligned} Q \\ unit: [J = Joule] \end{aligned}\]辐射通量
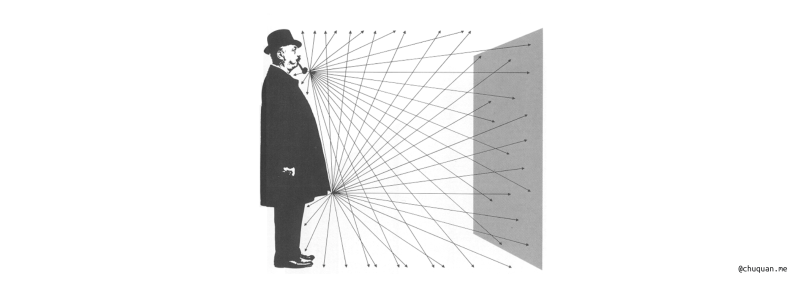
辐射通量(Radiant Flux)表示单位时间内流通(发射、反射、传输、接收)的能量,用符号 \(\Phi\) 表示,以 瓦特(W = Watt)或 流明(lm = lumen)为单位。在实际应用中,我们经常将辐射通量称为能量,本质上是因为辐射通量可以结合时间快速计算出辐射能量。
\[\begin{aligned} \Phi = \frac{dQ}{dt} \\ unit: [W = Watt]/[lm = lumen] \end{aligned}\]在光学物理中,我们也将辐射通量定义为 单位时间辐射出光子的数量。
辐射强度
辐射强度(Radiant Intensity)表示 单位立体角的辐射通量。其中 \(\Phi\) 表示辐射通量,\(\omega\) 表示立体角。我们可以用辐射强度描述一束光线,即形成一个锥体角度的光线,在单位时间内流通的能量。
\[\begin{aligned} I(\omega) = \frac{d\Phi}{d\omega} \\ unit: [\frac{W}{sr}][\frac{lm}{sr} = cd = candela] \end{aligned}\]
辐射照度
辐射照度(Irradiance)表示 单位(正交)面积的辐射通量。注意,这里计算的辐射通量必须与面垂直,如果光照不垂直于面,则计算其垂直分量。其中 \(\Phi\) 表示辐射通量,\(A\) 表示正交面积,$$ 表示位置。
\[\begin{aligned} E(p) = \frac{d\Phi(p)}{dA} \\ unit: [\frac{W}{m^2}][\frac{lm}{m^2} = lux] \end{aligned}\]
此时,我们回顾 《计算机图形学基础(5)——着色》 文中的兰伯特余弦定理,可以计算辐射照度,如下所示。
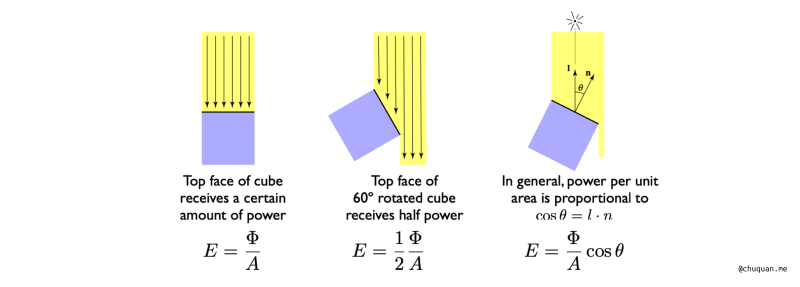
同样,我们还可以计算空间中一个点光源在空间中辐射的衰减到底是什么?如下所示,其实我们可以发现辐射照度随着半径增加而指数级衰减,辐射强度并没有发生变化。
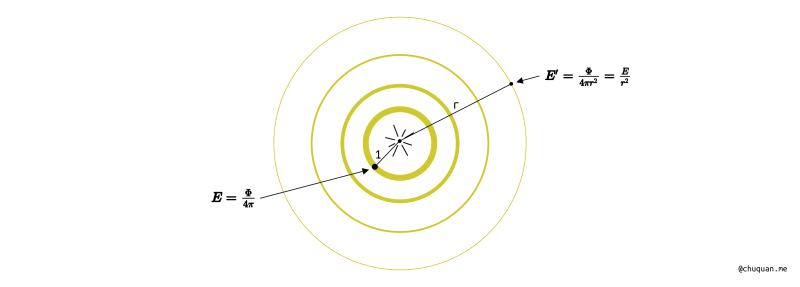
辐射亮度
辐射亮度(Radiance)表示 单位立体角、单位(正交)面积的辐射通量。辐射亮度一般用于描述光线在传输过程中的属性。我们可以用辐射亮度来描述某个面光源在某个(锥形)方向的辐射通量。
从定义上看,辐射亮度在立体角、正交面积两个维度做了两次微分。其中,\(cos\theta\) 表示光线在单位面积垂直方向上的角度分量,\(p\) 表示位置,\(\omega\) 表示立体角。
\[\begin{aligned} L(p, \omega) = \frac{d^2\Phi(p, \omega)}{d{\omega}dA cos\theta} \\ unit: [\frac{W}{sr m^2}][\frac{cd}{m^2} = \frac{lm}{sr m^2} = nit] \end{aligned}\]
下面,我们回顾一下辐射强度和辐射照度的定义。
- 辐射强度:单位立体角的辐射通量。
- 辐射照度:单位(正交)面积的辐射通量
结合辐射强度和辐射照度的定义,我们可以将辐射亮度的定义进行转换,单位立体角的辐射照度 或 单位(正交)面积的辐射强度。这两种定义正好可以应用到两种不同方向的辐射亮度,分别是 入射辐射亮度 和 出射辐射亮度。
入射辐射亮度
入射辐射亮度(Incident Radiance)即单位立体角的辐射照度。我们可以理解从某个方向向一个面进行辐射,该面所接收的辐射照度,如下图所示。如果我们进一步考虑来自四面八方的辐射,比如环境光,那么可以计算得到这个面所接收的全部辐射照度。
\[\begin{aligned} L(p, \omega) = \frac{dE{p}}{d{\omega} cos\theta} \end{aligned}\]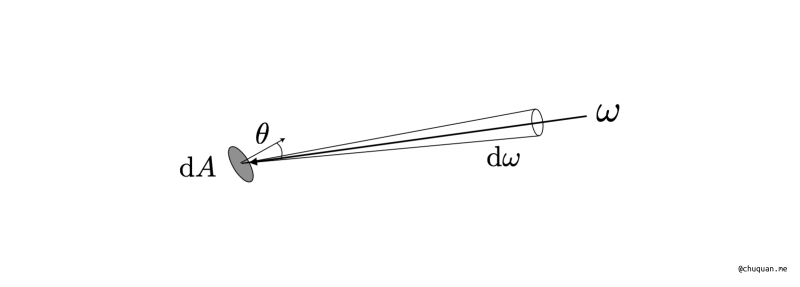
出射辐射亮度
出射辐射亮度(Exiting Radiance)即单位(正交)面积的辐射强度。我们可以理解一个面向某个方向进行辐射,该方向所发射的辐射强度,如下所示。如果我们进一步考虑一个面向四面八方的辐射,那么可以计算得到这个面所发射的全部辐射强度。
\[\begin{aligned} L(p, \omega) = \frac{dI(p, \omega)}{dA cos\theta} \end{aligned}\]
辐射照度 vs. 辐射亮度
在图形学中,辐射照度(Irradiance)和辐射亮度(Radiance)用的非常多。在下图所示的场景中,辐射照度表示 \(dA\) 接收的所有能量;辐射亮度表示 \(dA\) 从某个方向接收的能量。相比而言,辐射亮度是一个更细粒度的分析属性。这样,我们就把辐射照度和辐射亮度联系起来了。
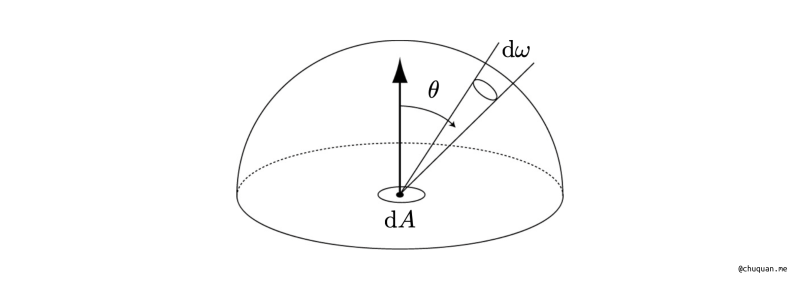
对于上图所示的场景,我们可以计算得到某个位置的辐射照度,如下所示,其中 \(H^2\) 表示单位半球面积。
\[\begin{aligned} dE(p, \omega) = & L_{i}(p, \omega) cos\theta d\omega \\ E(p) = & \int_{H^2} L_{i}(p, \omega) cos\theta d{\omega} \end{aligned}\]应用
双反射分布函数
已知入射光线的能量和角度,当辐射到物体表面后,光线会向各个角度反射,且各个角度反射的能量是不同的。双反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)就是用于计算这种场景下各个角度的反射能量。
如下所示,是一个入射和反射的场景,我们从辐射度量学的角度分别进行分析。
- 入射阶段:当入射光线从 \({\omega}_i\) 角度辐射到物体表面的一个位置时,可以认为该位置吸收了所有的光线能量,用辐射照度来表示,即 \(dE({\omega}_i)\)。
- 反射阶段:可以认为该位置将光线能量向各个方向进行辐射。对于方向 \({\omega}_i\) 的光线能量,用辐射亮度来表示,即 \(dL_r(x, {\omega}_r)\)。
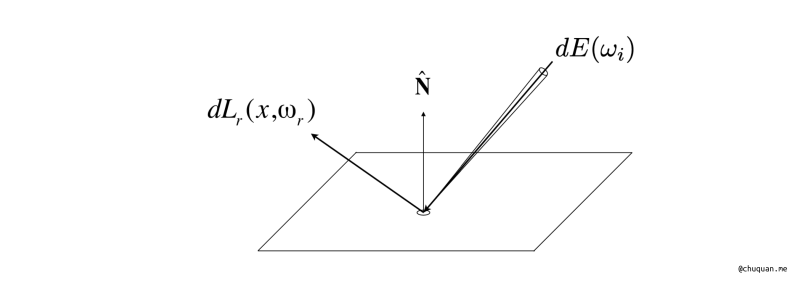
本质上,BRDF 就是表示由入射方向 \({\omega}_i\) 向反射方向 \({\omega}_r\) 辐射能量的比例函数 \(fr({\omega}_i \rightarrow {\omega}_r)\),其定义如下所示。
\[\begin{aligned} BRDF: f_r({\omega}_i \rightarrow {\omega}_r) = \frac{dL_r({\omega}_r)}{dE_i({\omega}_i)} = \frac{dL_r({\omega}_r)}{L_i({\omega}_i) cos{\theta}_i d{\omega}_i} \end{aligned}\]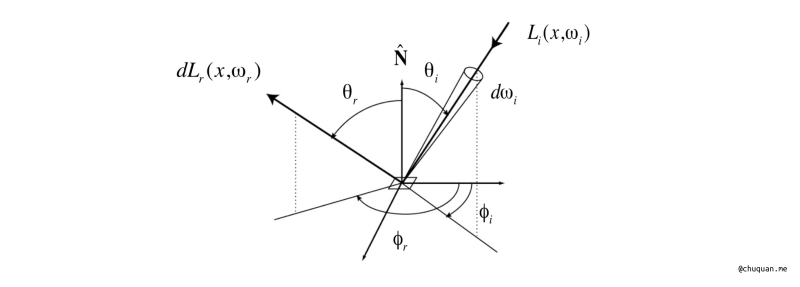
在实际应用中,对于镜面反射,BRDF 定义反射方向包含所有能量,其他方向均为 0;对于漫反射,BRDF 定义所有方向的能量分布相同。事实上,BRDF 就是描述了光线和物体表面的作用,也就是决定了物体的材质。
反射方程
基于 BRDF,我们可以进一步推导出 反射方程(The Reflection Equation)。
由于 BRDF 定义了一个入射方向 \({\omega}_i\) 向一个反射方向 \({\omega}_r\) 反射时的能量比例。那么,我们可以通过积分计算所有方向对一个反射方向 \({\omega}_r\) 的能量聚合。因此,我们可以推导得出如下所示的反射方程。
\[\begin{aligned} L_r(p, {\omega}_r) = \int_{H^2}f_r(p, {\omega}_i \rightarrow {\omega}_r) L_i(p, {\omega}_i) cos{\theta}_i d{\omega}_i \end{aligned}\]
渲染方程
基于反射方程,我们还可以进一步推导出 渲染方程(The Rendering Equation)。
这里我们只需要额外考虑物体本身会发光的情况,于是增加一个发光项即可得到渲染方程,如下所示。其中,\(cos{\theta}_i\) 转换成了法向量和入射方向的点积 \(n \cdot {\omega}_i\)。现代图形学中,所有基于表面反射的渲染都是基于该渲染方程实现的。
\[\begin{aligned} L_r(p, {\omega}_r) = L_e(p, {\omega}_r) + \int_{H^2} L_i(p, {\omega}_i) f_r(p, {\omega}_i, {\omega}_r)(n \cdot {\omega}_i) d{\omega}_i \end{aligned}\]总结
本文我们主要介绍了辐射度量学中的几个概念:辐射能量、辐射通量、辐射强度、辐射照度、辐射亮度等。基于这些概念,我们引入了 BRDF 的定义。然后依次推导出反射方程和渲染方程。
参考
- 《GAMES 101》
